This may not be the first time someone recognized this, but I have recently discovered some interesting and useful properties of the entropy function and now share them.
Definition
Entropy — H(p₁, p₂, …, pₙ) — is a function that quantifies surprise in selecting an object from a set where the probability of selecting each object is given: {p₁, p₂, …, pₙ}. This has utility in communications, information theory, and other fields of math.
Hᵦ(p₁, p₂, …, pₙ) = Σ(i..n) -pᵢ logᵦ(pᵢ)
Where b is normally 2, to express entropy in bits.
Other definitions of H() use expected values and random variables. As an analog to the definition above, I will discuss entropy of a set of frequencies:
pᵢ = fᵢ / Σ fᵢ.
Entropy defined without bits
A definition that doesn’t use bits is:
H(p₁, p₂, …, pₙ) = Π(i..n) pᵢ⁻ᵖⁱ
You can convert between the definitions with Hᵦ = logᵦ H. H() is also called perplexity.
A recursive (associative) definition of entropy
The entropy function is associative, or can be applied recursively. Consider the function as applying to frequencies (rather than probabilities).
If we have the frequencies f = {17, 24, 16, 0, 9}, we can find the entropy H(f) if we have a bifurcation of the set fₐ + fᵦ = f, entropy of the bifurcations H(fₐ), H(fᵦ), and the total of each set’s frequency, Σ fₐ, Σ fᵦ.
Hᵦ(fₐ + fᵦ) = Hᵦ(fₐ) Σ fₐ / (Σ fₐ + Σ fᵦ) + Hᵦ(fᵦ) Σ fᵦ / (Σ fₐ + Σ fᵦ) + Hᵦ({Σ fₐ, Σ fᵦ})
One case of the above definition is when fᵦ contains a single element, i. (We use t = Σ fₐ hereafter.)
Hᵦ(fₐ + i) = Hᵦ(fₐ) t / (t + i) + t / (t + i) logᵦ[(t + i) / t] + i / (t + i) logᵦ[(t + i) / i]
Without bits, the equivalent is:
H(fₐ + i) = H(fₐ)ᵗ/(t+i) * (t + i) / iⁱ/(t+i) * (t + i) / tᵗ/(t+i)
An iterative definition of entropy
Entropy can be defined directly from the symbol frequencies fᵢ, not probabilities pᵢ. This is useful in computations where the entire symbol set is not known in advance and you want to avoid two passes (one to find the total, one to calculate), especially in parallel processing, or where arithmetic is expensive and precalculation will be used.
Hᵦ(f₁, f₂, …, fₙ) = logᵦ(t) - 1/t Σ(i..n) fᵢ logᵦ(fᵢ)
For completeness, the iterative definition of entropy without bits is:
H(f₁, f₂, …, fₙ) = t (Π(i..n) fᵢᶠⁱ)⁻¹/ᵗ
Entropy visualization
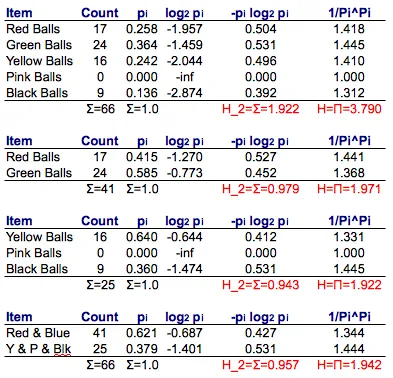
▧
Comments
Another great resource: https://www.mtm.ufsc.br/~taneja/book/node6.html
William Entriken
Please discuss this topic anywhere and let me know any great comments or media coverage I should link here.